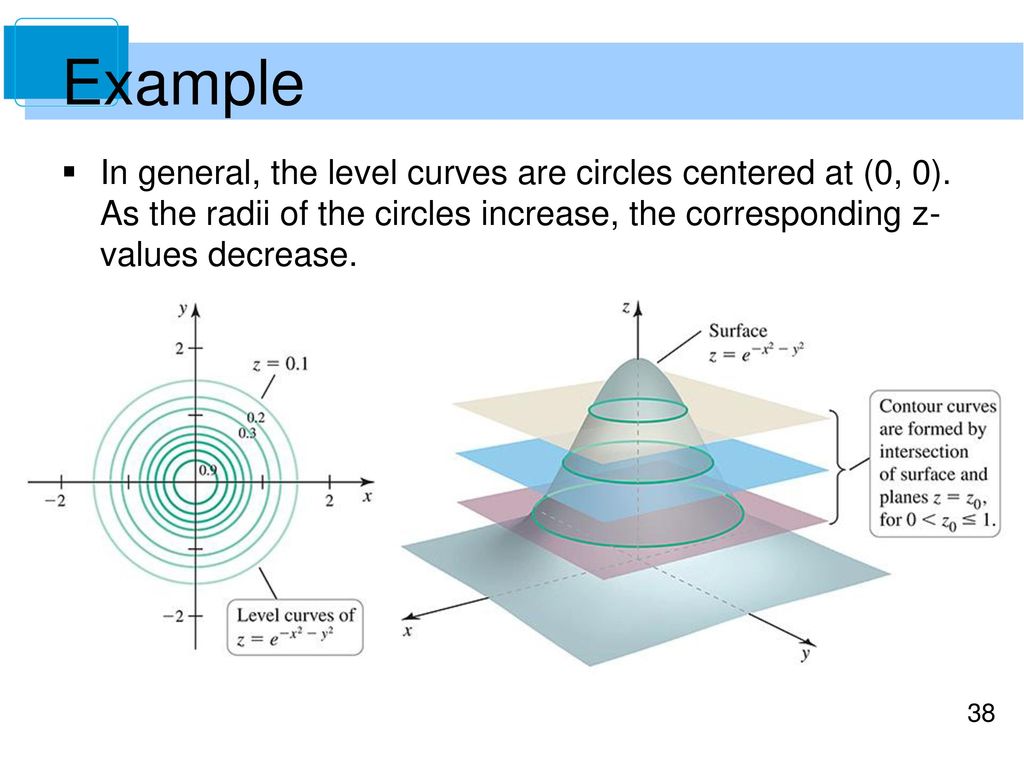
One common example of level curves occurs in topographic maps of mountainous regions, such as the map in Figure 2 The level curves are curves of constant elevation Notice that if you walk along one of these contour lines you neither ascend nor descend FigureLevel curves are in the xy plane One level curve consists eg of all (x,y) points which satisfy f(x,y)=100 If , then this level curve will be the circle Another level curve will be the circle , etc A contourplot is a 2d representation of a 3d surface, just like a flat (ie, 2d) map is a representation of the 3d mountains9 Level Curves and Level Surfaces (Section S 143 1 day) Outcomes A Represent a function of two variables by level curves B Represent a function of three variables by level surfaces C Determine the level curve or surface of a function through a given point D Match the graph of a surface with the graph of its level curves Reading

L7 Evaluation Of Functions Domain And Range Level Curves And Surfaces Ppt Level Curves And Level Surfaces Math23 Multivariable Calculus General Course Hero
Level curves and level surfaces
Level curves and level surfaces-One way to sketch a 3d surface is to plot crosssections for several values of one variable Then plot crosssections for several values of the other variableLevel surfaces For a function w = f ( x, y, z) U ⊆ R 3 → R the level surface of value c is the surface S in U ⊆ R 3 on which f S = c Example 1 The graph of z = f ( x, y) as a surface in 3 space can be regarded as the level surface w = 0 of the function w ( x, y, z) = z − f ( x, y)



Ex8 Klaus Schmitt Webwork Problems 1 1 Pt Compute The Gradient Vector Elds Of The Following Functions A F X Y 6x2 10y2 F X Y 12xi yj B F X Y Course Hero
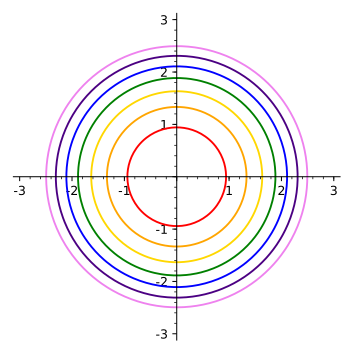
Ie the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below is the surface Examine the level curves of the functionA level curve, or surface, is a set on which f is constant If you are on a level curve, and you want to stay on that curve, which way should you travel?Level curves and contour plots are another way of visualizing functions of two variables If you have seen a topographic map then you have seen a contour plot Example To illustrate this we first draw the graph of z = x2 y2 On this graph we draw contours, which are curves at a fixed height z = constant For example the curve at height z = 1 is the circle x2 y2 = 1 On the graph we have
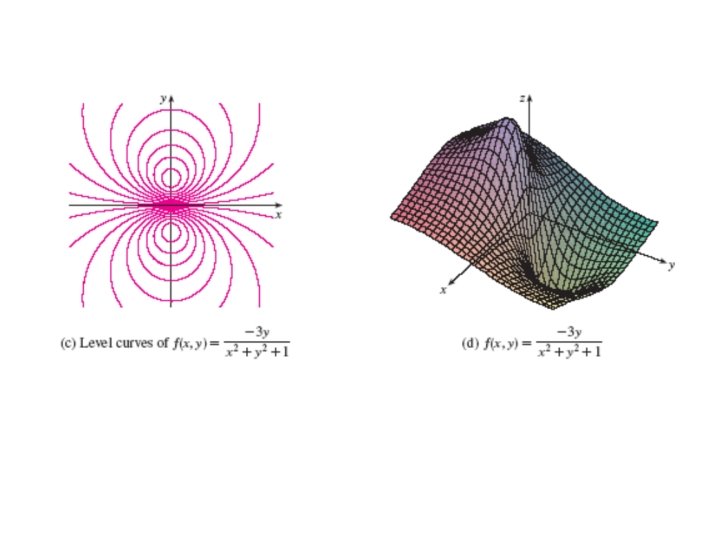
P Sam Johnson (NIT Karnataka) Normals to Level Curves and Tangents September 1, 19 2 / 30 Tangent Planes and Normal Lines If r = g(t)i h(t)j k(t)k is a smooth curve on the level surfaceSurface will be e ected by continuous deformations Our main interest are curves and surfaces These are special cases of manifolds Roughly, a manifold can be understood as a gluing together of various pieces of at material Curves are images of a mapC Graph the level curve AHe, iL=3, and describe the relationship between e and i in this case T 37 Electric potential function The electric potential function for two positive charges, one at H0, 1L with twice the strength as the charge at H0, 1L, is given by fHx, yL= 2 x2 Hy1L2 1 x2 Hy 1L2 a Graph the electric potential using the window @5, 5Dµ@5, 5Dµ@0, 10 D
With this ability, you could flow across continuouslyspaced level curvesIe the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below is the surface Examine the level curvesI'm studying about the functions and one chapter is about level sets, curves and surfaces Is there a software which can help me to generate automatically level curves Also if you can help me with the graph of $\displaystyle z=x^2y^2$ and its level curves Thanks )



3 D Calculus Continuous Function Function Mathematics



Math 13 Lecture Drawing Surfaces Level Curves Contour Maps And Pa Oneclass
From the definition of a level curve above, we see that a level curve is simply a curve of intersection between any plane parallel to the $xy$axis · These level curves and gradient vector fields are slowly building an outline of a surface in \( \mathbb{R}^3\) However, we are still lacking a way of connecting the curves and the arrows How would one follow the vectors to get from one level curve to the next?A level curve of the surface is a twodimensional curve with the equation, where k is a constant in the range of f A level curve can be described as the intersection of the horizontal plane with the surface defined by f Level curves are also known as contour lines



14 Partial Derivatives Copyright Cengage Learning All Rights



Level Surfaces
Using the mountain analogy, determine the direction of maximum slope and turn 90° This takes you neither up hill nor down hill, but along the side of the mountain · The following routine plots the level surfaces of the function f(x, y, z) = for w = 1 , 4 and 9, for x and y ranging between 3 and 3 with z positive Try executing it (place the cursor at the end and press the Enter key) (Note it takes considerable time to complete all the computations!) (* Mathematica Routine to plot level curves of f (xWe can "stack" these level curves on top of one another to form the graph of the function Below, the level curves are shown floating in a threedimensional plot Drag the green point to the right



Level Sets Math Insight


Introduction To Functions Of Several Variables Ppt Download
· It seems much more natural to define our curve as a level surface of a function of two variables, but doing that, as you've seen, doesn't work, and I don't quite know why multivariablecalculus curves Share Cite Follow edited Feb 26 '19 at 1949 PeatherfedLevel Curves and Surfaces Example 1 In mathematics, a level set of a function f is a set of points whose images under f form a level surface, ie a surface such that every tangent plane to the surface at a point of the set is parallel to the level setLevel curves and surfaces The level curves of are curves in the plane along which has a constant value The level surfaces of are surfaces in space on which has a constant value Sometimes, level curves or surfaces



Math 2110 Section 13 1 Level Curves And Level Surfaces Youtube



Mitres 18 001 Guide13 Matematica
Graph and level curves/surfaces (Sec 141) Limits and continuity (Sec 142) x z f(x,y) y Slide 2 ' & $ % Scalar functions of 2 variables is denoted as f(x;y) De nition 1 A scalar function fof two variables (x;y) is a rule that assigns to each ordered pair (x;y) 2DˆIR2 a unique real number, denoted by f(x;y), that is, f DˆIR2!RˆIR · Plot level curves, at level 1,2,3 and 4, for the surfaces below using contour Use a meshgrid(052)Always perpendicular to the contour curves marking out the surface as it increases away from the center The gradient tells us the missing information about the third dimension, which is the direction of increase The spacing of level curves themselves can give us information about the rate of increase



Pdf An Adaptive Algorithm For Efficient Computation Of Level Curves Of Surfaces


12 1 Introduction To Multivariable Functions Mathematics Libretexts
So again, we want to try to do visualize the level surfaces dysfunction And so you could pick anything you wanted Let's say we picked K equaling zero In other words, on the set of all pointsSo a level curve is the set of all realvalued solutions of an equation in two variables x1 and x2 When n = 3, a level set is called a level surface (see also isosurface), and for higher values of n the level set is a level hypersurfaceThe former leads to the study of curves and surfaces, and the latter leads to the study of solid modeling This high level overview focuses on the former It starts by reviewing some common applications of curve and surface modeling, and then moves on to mathematical representations


Applications Of Gradient The Directional Derivative Suppose We


Calcplot3d An Exploration Environment For Multivariable Calculus Level Surfaces
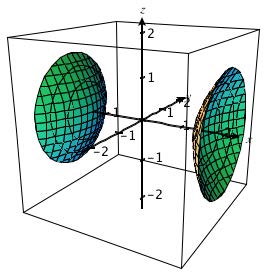
Many surfaces can be described as level surfaces If this is the case, we call this an implicit description of a surface Here are some examples we know already Spheres The level surfaces of g(x,y,z) = x2 y2 z2 are spheres Graphs For g(x,y,z) = z − f(x,y) we have the level surface g = 0 which is the graph z = f(x,y) of a function of two variablesLevel Curves (ie Contours) and Level Surfaces Consider a function For any constant we can consider the collection of points satisfying the equation This collection of points is generally called a level surfaceWhen we generically have a (true 2dimensional) surface For example The level surface of at level is the unit sphere (the sphere of radius 1 centered at the origin)Using the information on the topology of the level curves of the surface wrt the variables x, y, z, we provide an algorithm to compute a box of this kindThe fourth application is a symbolicnumeric algorithm to compute the connected components of a surface by using level curves



Visualizing Surface And Level Curves Youtube


12 5 Functions Of Three Variables
The level curves (or contour lines) of a surface are paths along which the values of z = f (x,y) are constant;Level Surfaces Given w = f(x,y,z) then a level surface is obtained by considering w = c = f(x,y,z) The interpretation being that on a level surface f has the same value at every pt For example f could represent the temperature at each pt in 3space Then on a level surface the temperature is the same at every pt on that surfaceA level curve can be drawn for function of two variable ,for function of three variable we have level surface A level curve of a function is curve of points where function have constant values,level curve is simply a cross section of graph of f
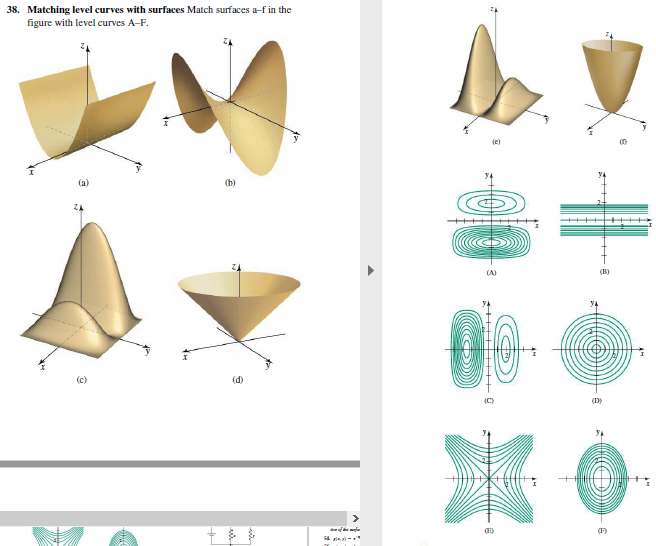


Solved Matching Level Curves With Surfaces Match Surfaces Chegg Com
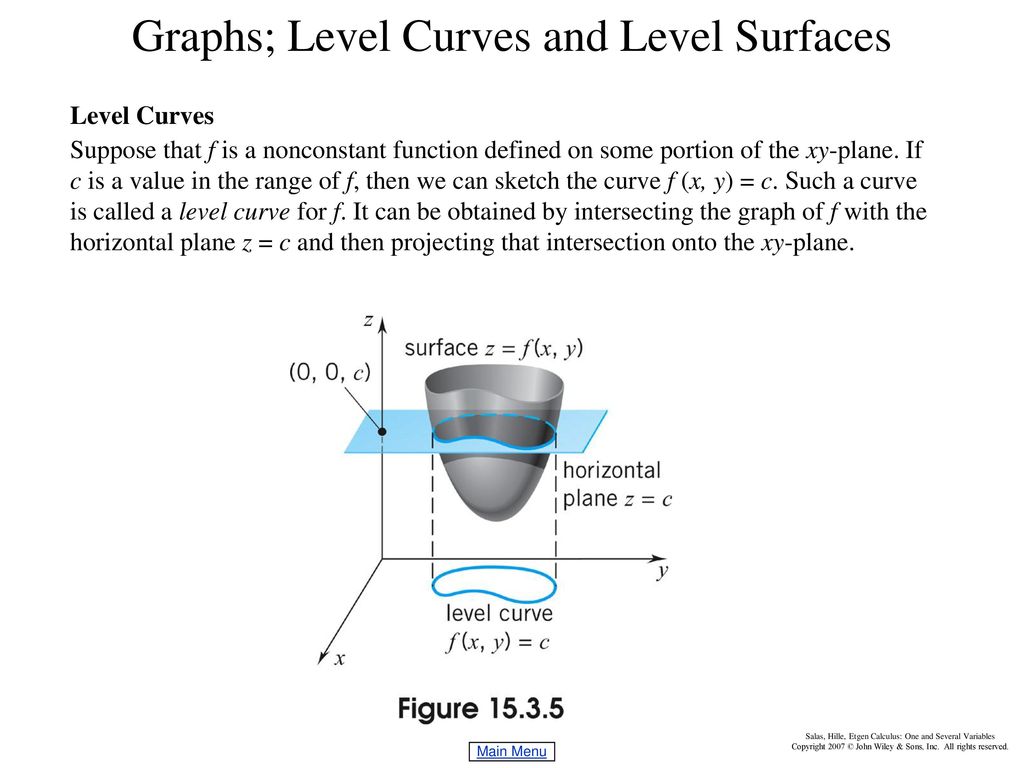


Chapter 15 Functions Of Several Variables Ppt Download
Different kind of systems tracts are assigned on the basis of stratal stacking pattern, position in a sequence and in the sea level curve and types of bounding surfaces 4 A lowstand systems tract (LST) forms when the rate of sedimentation outpaces the rate of sea level rise during the early stage of the sea level curveLevel curves for a function $z=f (x,\,y) \, D \subseteq {\mathbb R}^2 \to {\mathbb R}$ the level curve of value $c$ is the curve $C$ in $D \subseteq {\mathbb R}^2In two dimensions, the gradient was orthogonal to the level curves Thus, in three dimensions, one would hope that the gradient is orthogonal to the level surfaces Thus, in three dimensions, one would hope that the gradient is orthogonal to the level surfaces



Split Surface With Multiple Curves Revit Dynamo



Calc 501 1000 By James Bardo Issuu
Level Curves and Surfaces The graph of a function of two variables is a surface in space Pieces of graphs can be plotted with Maple using the command plot3d For example, to plot the portion of the graph of the function f(x,y)=x 2 y 2 corresponding to x between 2 and 2 and y between 2 and 2, type > with (plots);Level Curves and Contour Maps The level curves of a function f(x;y) of two variables are the curves with equations f(x;y) = k, where kis a constant (in the range of f) A graph consisting of several level curves is called a contour map Level Surfaces The level surfaces of a function f(x;y;z) of three variables are the surfaces · Level curves on surface in OpenGL Ask Question Asked 2 years, 11 months ago Active 2 years, 11 months ago Viewed 640 times 0 I have a function f defined on a triangle mesh, ie for each vertex, I have an associated number For example, f could be the geodesic distance on the mesh, ie f(x)=d(a,x) computed for each point in the mesh, from



L7 Evaluation Of Functions Domain And Range Level Curves And Surfaces Ppt Level Curves And Level Surfaces Math23 Multivariable Calculus General Course Hero


The Gradient And Directional Derivative
Parametrized curves and surfaces 3 Example 114 The space curve γ(t) = (λt,rcos(ωt),rsin(ωt)), where r>0 and λ,ω6= 0 are constants, is called a helix It is the spiraling motion of a point which moves along the xaxis with velocity λwhile at the same time rotating around this axis with radius rand angular velocity ω z y x 12 SurfacesA level set of a function of two variables f ( x, y) is a curve in the twodimensional x y plane, called a level curve A level set of a function of three variables f ( x, y, z) is a surface in three · The contour will represent the intersection of the surface and the plane For functions of the form \(f\left( {x,y,z} \right)\) we will occasionally look at level surfaces The equations of level surfaces are given by \(f\left( {x,y,z} \right) = k\) where \(k\) is any number The final topic in this section is that of traces In some ways these


14 1 Functions Of Several Variables



Exact And Approximated Magnetic Field Lines Realised As Level Curves Download Scientific Diagram
LEVEL CURVES The level curves (or contour lines) of a surface are paths along which the values of z = f(x,y) are constant;Gradient proof that it is perpendicular to level curves and surfaces Let w = f(x,y,z) be a function of 3 variables We will show that at any point P = (x 0,y 0,z 0) on the level surface f(x,y,z) = c (so f(x 0,y 0,z 0) = c) the gradient f P is perpendicular to the surfaceThe level curves of this function are ellipses centered at (1, 2) The semimajor axis of each ellipse is vertical and the semiminor axis is horizontal That is, the ellipses are taller than they are wide, and so this option doesn't match the given set of curves



Functions Of Several Variables Ppt Video Online Download
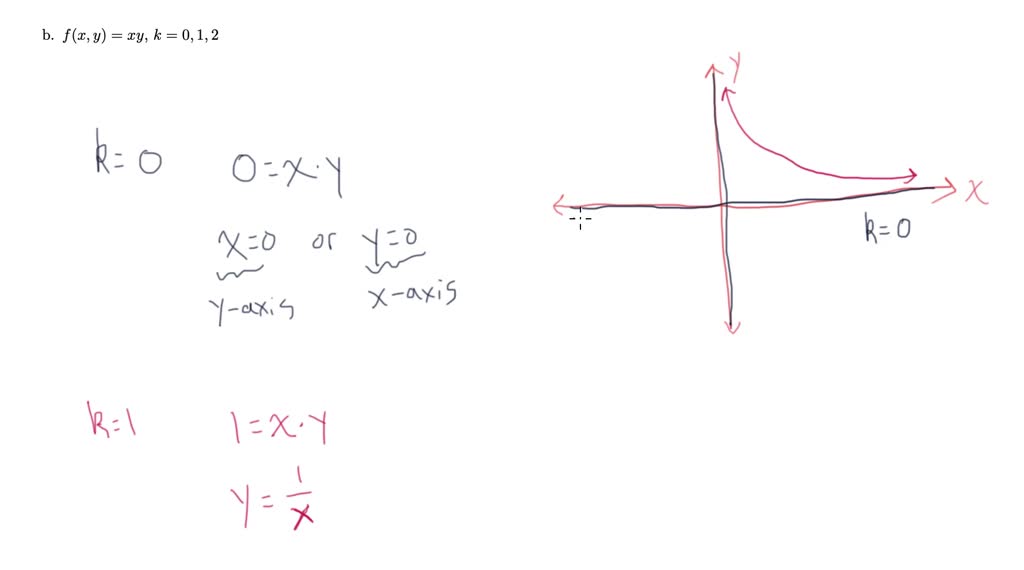


Level Curves And Surfaces Example 2 Numerade
Upon successful completion of this topic, you will be able to • explain what is meant by the domain and range of a function of several variables • sketch some of the level curves for a given surface • sketch some simple surfaces eg planes, cones, paraboloids, cylinders and spheres Screen 2 of 2 c °03 Department of Mathematics andMath 2110 Section 131 Level Curves and Level SurfacesLevel Curves and Level Surfaces The Smart BunnyA very short story by Kurt Vonnegut Jr Send an email regarding this site to Connie Liakos Evers, Kelly's sister (no math questions, please)


Level Curves And Contour Plots Mathonline



Level Curves Of Functions Of Two Variables Youtube


Level Sets The Gradient And Gradient Flow Project Project



Solved 15 1 Graphs And Level Curves 927 A Figure 15 18 Chegg Com



Level Curves



Constructing 3d Surfaces From Random Sets Of Points By Means Of Level Curves Scientific Net
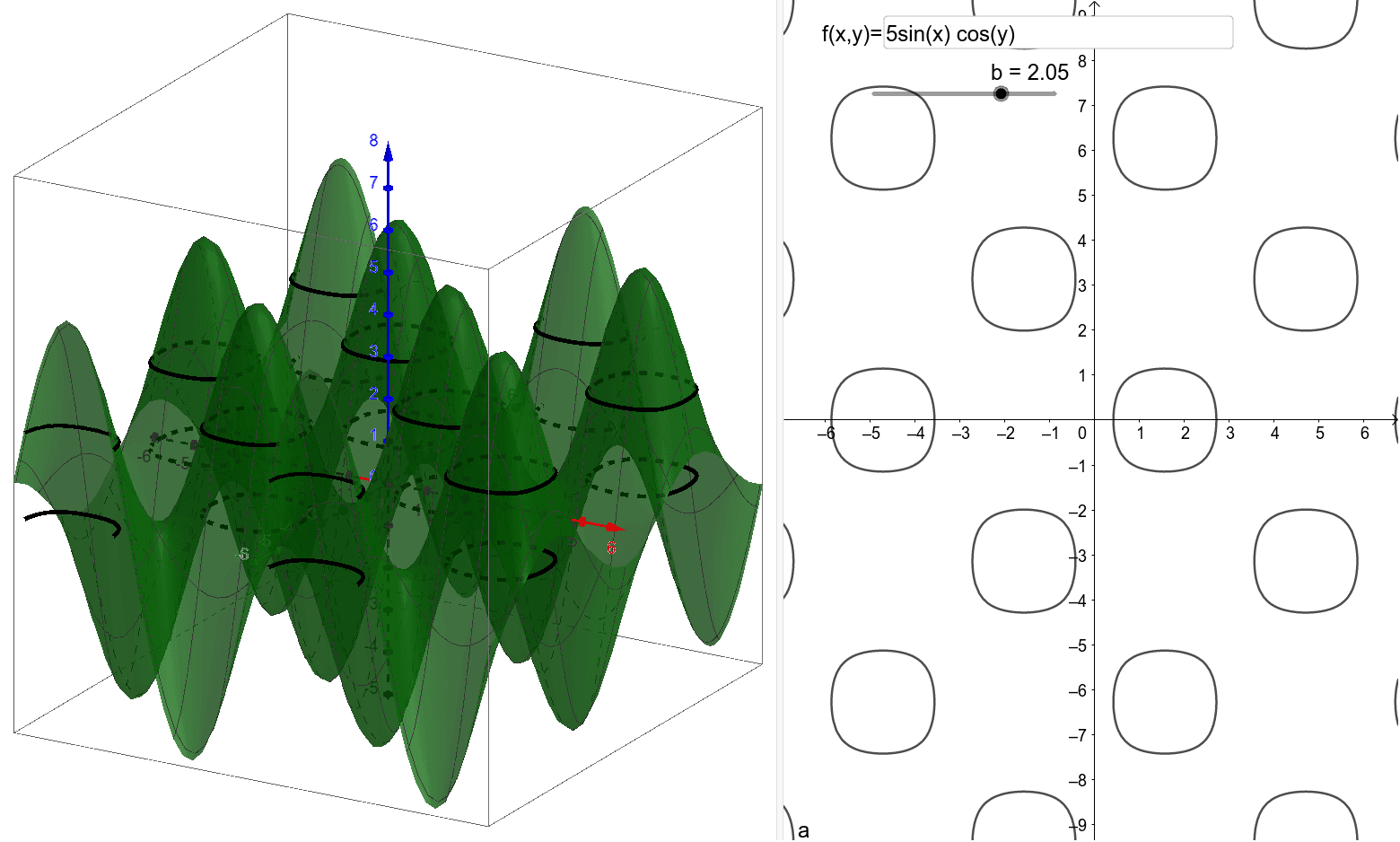


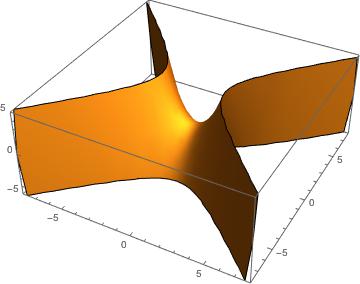
Level Curves And Surfaces Geogebra



Level Surfaces
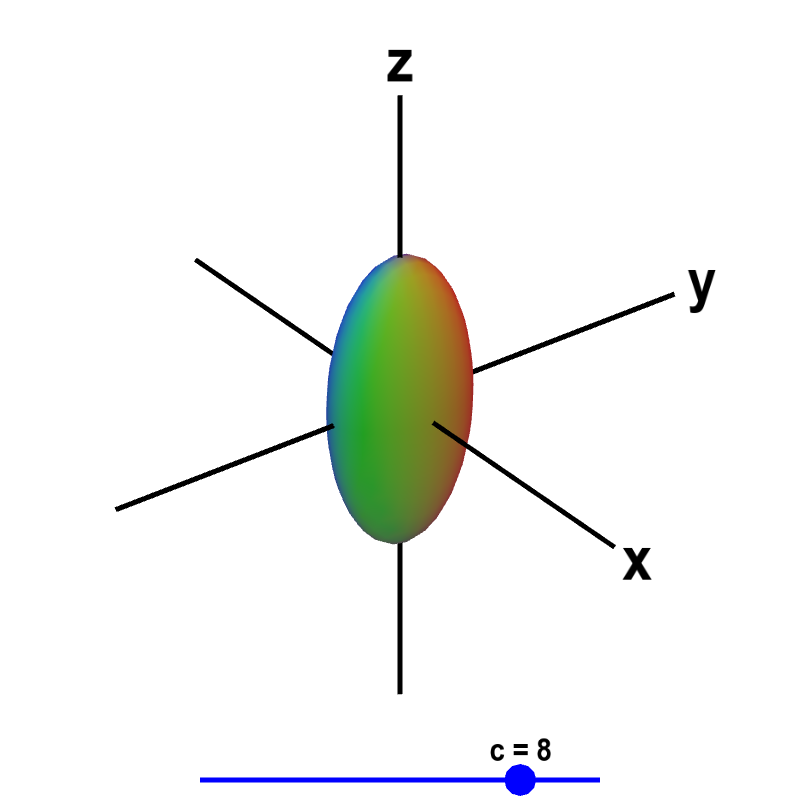


Level Sets Math Insight
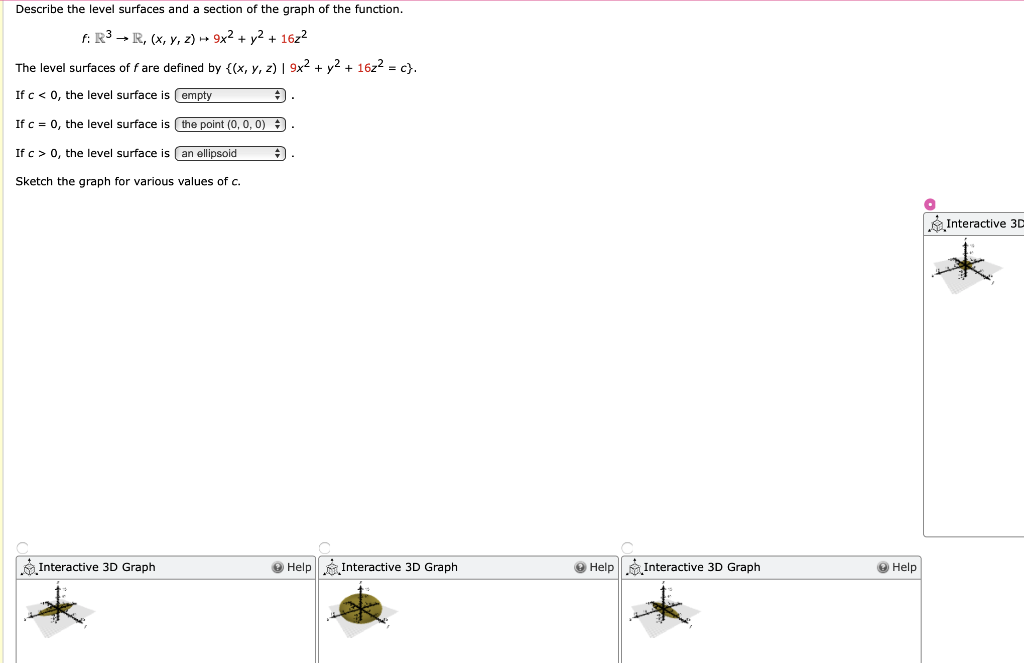


Solved Describe The Graph Of The Function By Computing So Chegg Com



Pdf Applications Of Level Curves To Some Problems On Algebraic Surfaces



Ex8 Klaus Schmitt Webwork Problems 1 1 Pt Compute The Gradient Vector Elds Of The Following Functions A F X Y 6x2 10y2 F X Y 12xi yj B F X Y Course Hero



Level Curves
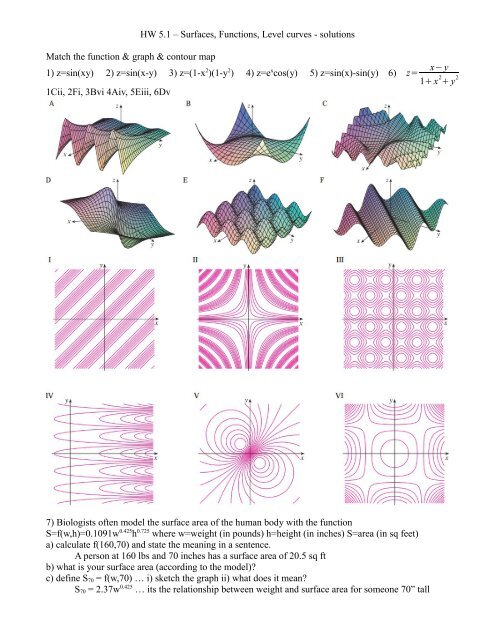


Hw 5 1 A Surfaces Functions Level Curves Solutions Match The
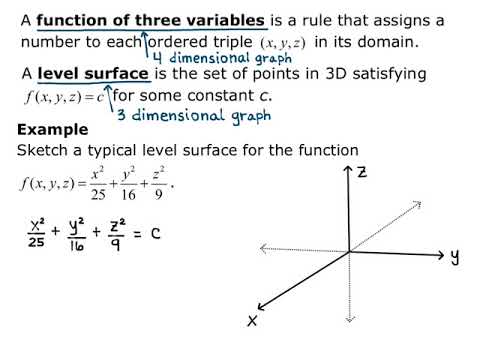


Section 13 1 Level Surfaces Youtube



On The Implicit Function Theorem And The Gradient Mathematics Stack Exchange


0 3 Visualizing Functions Of Several Variables



Gate Ese Level Curves And Surface Of A Function In Hindi Offered By Unacademy
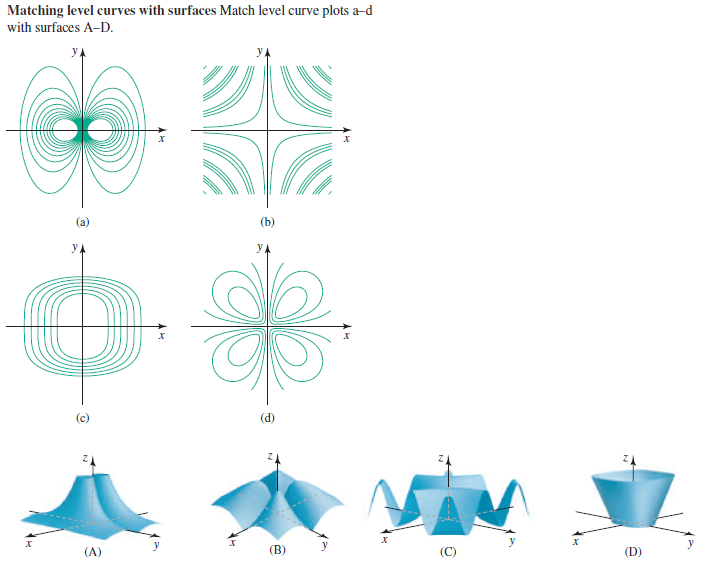


Answered Matching Level Curves With Surfaces Bartleby



Level Curves Mit 18 02sc Multivariable Calculus Fall 10 Youtube



Level Set Wikipedia
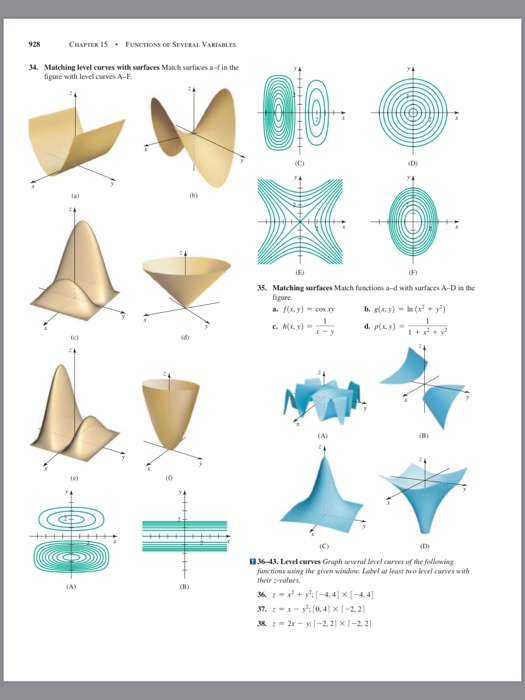


Solved 15 1 Graphs And Level Curves 927 A Figure 15 18 Chegg Com



Level Sets Math Insight


Level Curves And Contour Plots



Level Set Wikipedia



Level Set Wikipedia
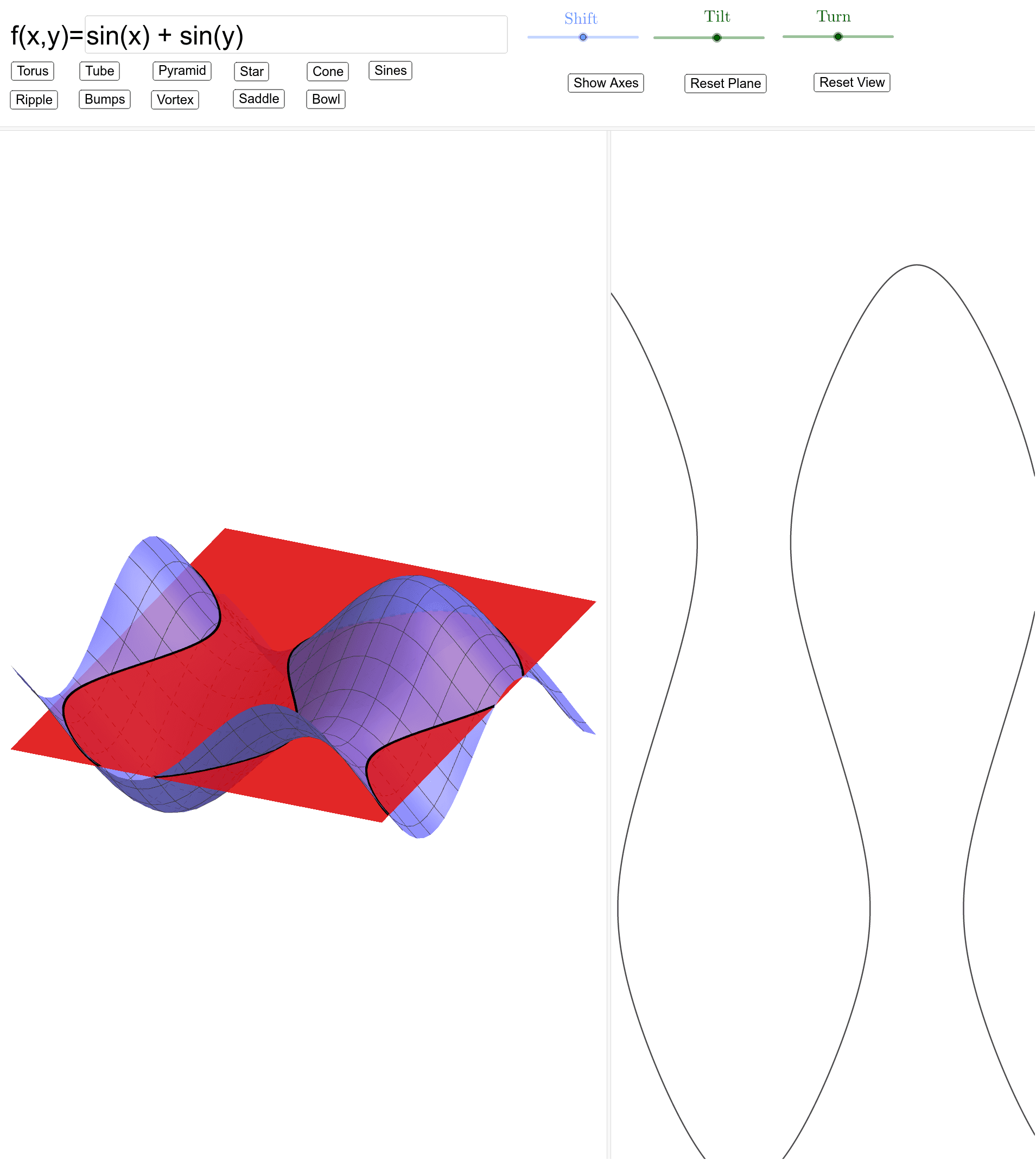


Level Curves From 3d Surfaces Geogebra



Calculus Iii Functions Of Several Variables
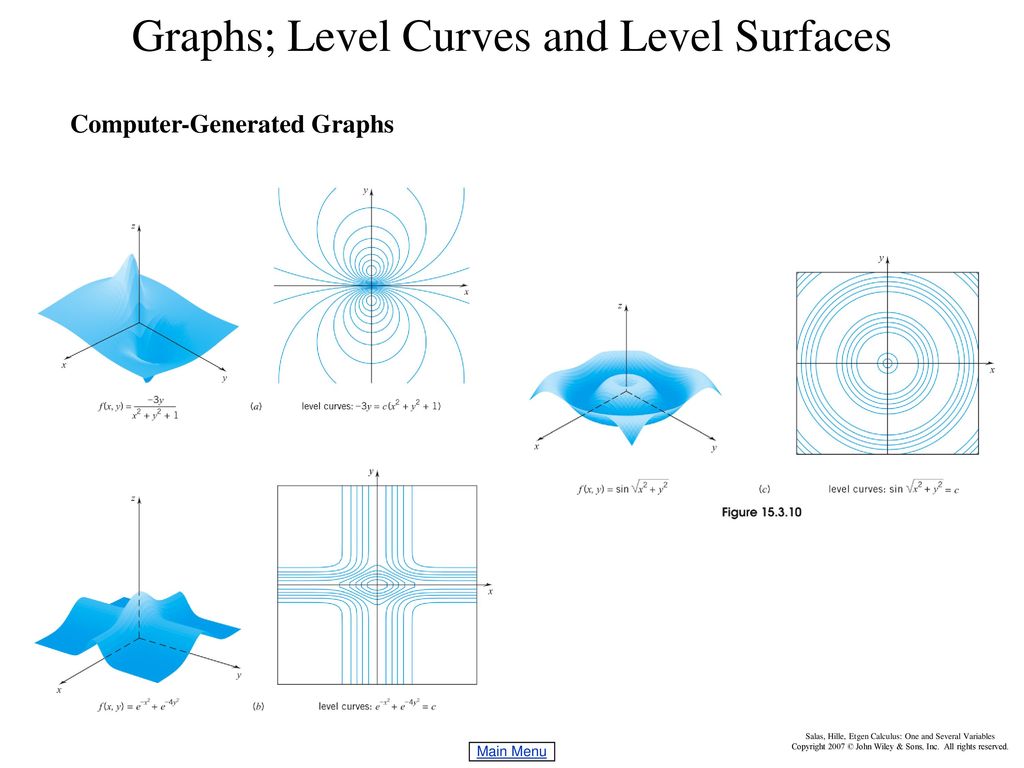


Chapter 15 Functions Of Several Variables Ppt Download



Level Curves And Surfaces Example 1 Numerade



Answered Question 1 Describe And Sketch The Bartleby



Document


Animated Demonstrations For Multivariable Calculus



Chapter 15 Functions Of Several Variables Ppt Download


Level Curves And Contour Plots Mathonline



Level Set Wikipedia



Level Surfaces In Matlab



Calculus Iii Functions Of Several Variables



Calculus Iii Functions Of Several Variables



Math Tutor Extra Functions Of More Variables


Gradients And Level Curves



Calculus Iii Functions Of Several Variables



14 1 Functions Of Several Variables Mathematics Libretexts



Level Set Examples Math Insight



Solved Take Home Quiz Level Curves And Level Surfaces Fo Chegg Com
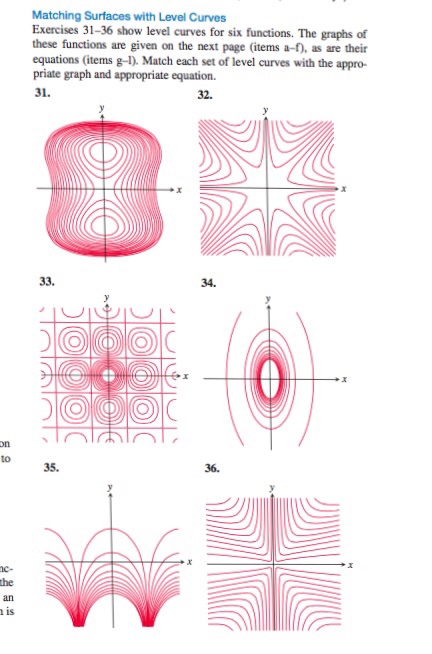


Solved Matching Surfaces With Level Curves Exercises 31 3 Chegg Com



Calculus Iii
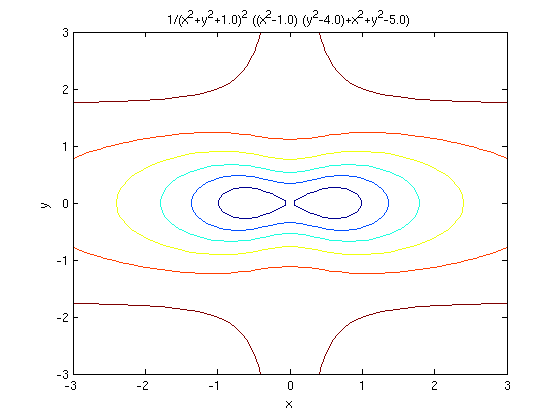


Visualizing Functions Of Several Variables And Surfaces
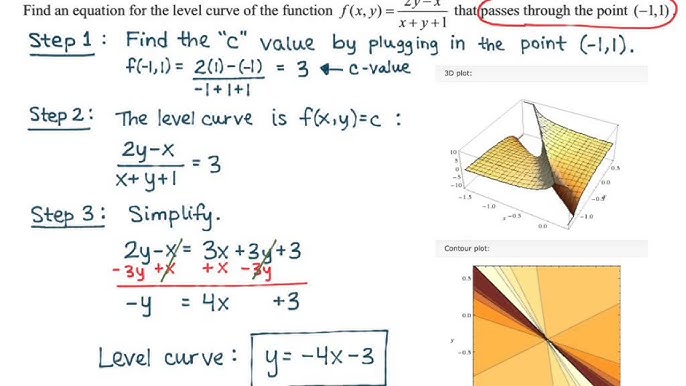


Math 2110 Section 13 1 Level Curves And Level Surfaces Youtube
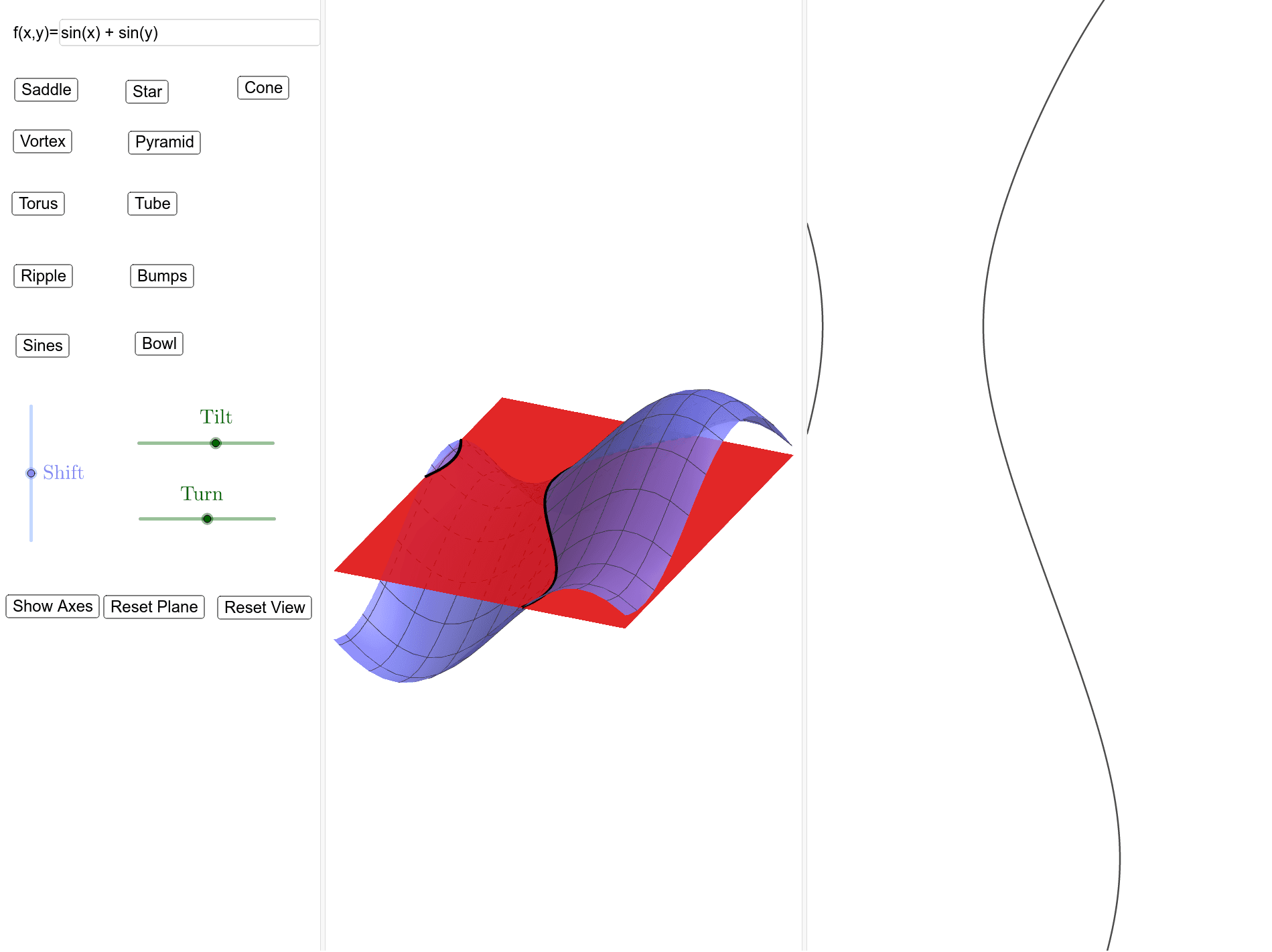


Level Curves From 3d Surfaces Different Layout Geogebra
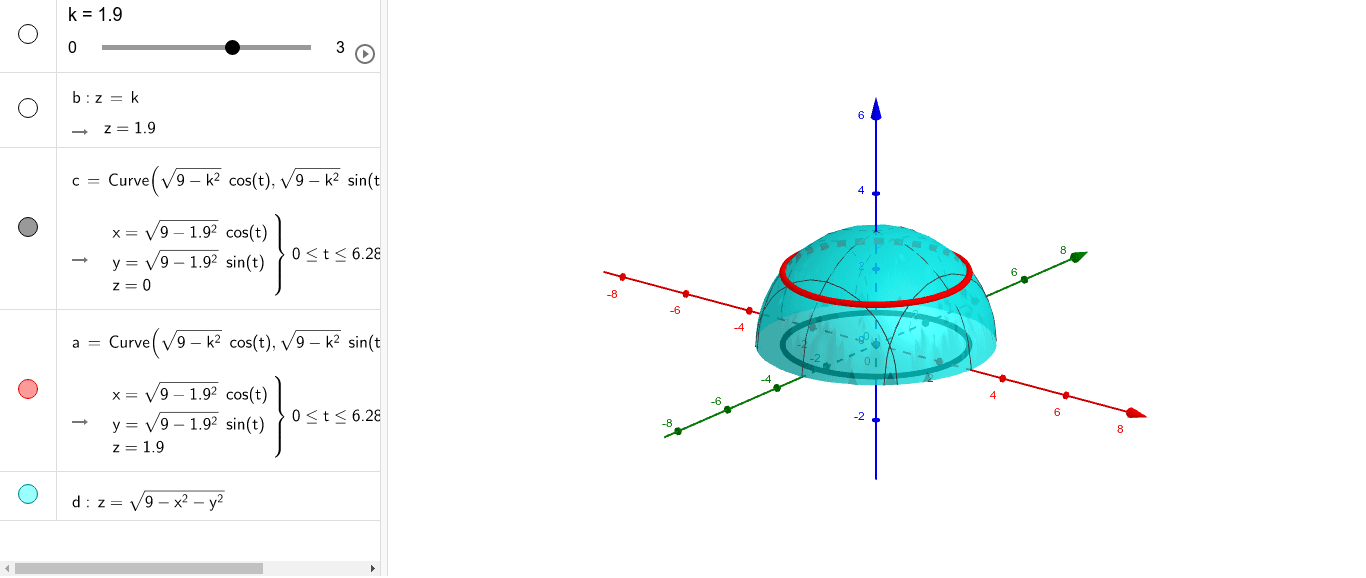


Sec 14 1 Level Curves And Surfaces Geogebra



Grad Perpndclr To Surface



Applications Of Gradient The Directional Derivative Suppose We



Level Curves



Level Sets Math Insight



Mathematics 3 Partial Differentiation Uia Logo Main Menu Calculator Partial Differentiation Introduction Application Contour Curves Application Aircraft Noise Application Temperature Application Electric Resistance Ordinary Differentiation Def



Level Curves And Cross Sections Maple Programming Help



Solved Describe The Level Curves Of The Function Z X2 Chegg Com



How To Sketch Level Curves Youtube



Document



Level Set Examples Math Insight



Aop And Atp Surfaces Level Curves Awt And Number Of Trains Behavior Download Scientific Diagram


Terrain From Level Curves Mesh Drape Grasshopper



Level Curves



Level Curve And A Surface Tex Latex Stack Exchange
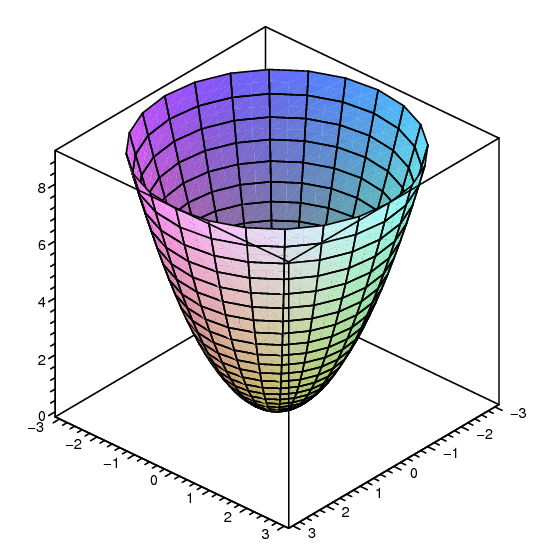


14 1 Functions Of Several Variables



0 件のコメント:
コメントを投稿